a/(b+c) + b/(c+a) + c/(a+b) = 4 的简单解释

作者：维塔利克·布特林 2025 年 5 月 11 日 原文链接

你可能在某个时候见过这个数学谜题：

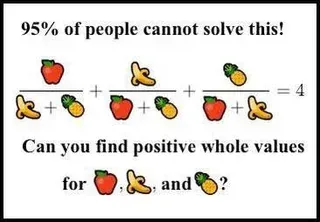
这个谜题在互联网上因为某些原因而出名，因为它看起来必须是简单的、不可能的，或者是一个陷阱问题（解决P = NP？哈哈，答案是N = 1，抓到你了！），但实际上这三种情况它都不是。这个问题就是它表面看起来的那样。这个问题是可解的。然而最小的解竟然是：

a = 154476802108746166441951315019919837485664325669565431700026634898253202035277999
b = 36875131794129999827197811565225474825492979968971970996283137471637224634055579
c = 4373612677928697257861252602371390152816537558161613618621437993378423467772036

这究竟是怎么回事？！如果你在互联网上搜索，你会看到冗长的解释，说这个问题实际上与椭圆曲线有关，以及来自代数几何的其他你从未听说过的花哨术语，即使你认为自己对椭圆曲线了如指掌，因为你是一个~密码学家~加密爱好者。

这篇文章的目标将是对这个谜题给出一个最基础的解释，不依赖于对这些概念的任何预先知识。

先不要求正值解决，然后再找正值解

首先，让我们从问题的一个宽松版本开始。具体来说，让我们去掉三个值必须为正的要求。事实证明，你可以通过纯人工暴力尝试各种可能性，得到两个答案：(1,2,3)和(1,1,1)。你可以通过重新排列数字、改变符号和乘以常数因子（例如，(2,4,6)也是一个有效解）从这两个答案中获得更多解，但我们将这些视为相同的解。

现在，我们进入有趣的部分。如果我们能想出一种方法来组合两个解并得到一个全新的第三个解呢？在数学中，这通常是可能的：如果你有两个5的倍数，它们的和也是5的倍数。更非平凡的例子是，如果你在圆上有两个有理点（即x和y满足x²+y²=1），你可以使用点加法定律创建圆上的第三个有理点：(x₁y₂+x₂y₁, y₁y₂-x₁x₂)。

如果我们能为我们的问题想出这样一个算法，那么我们就可以一次又一次地使用它，直到最终我们通过纯粹的运气得到一个全是正值的点。这将是我们的解决路径。

结合两个解找到第三个解

让我们通过只保留两个变量 x 和 y 来简化问题。注意这个方程是齐次的：它具有这样的特性，即按相同的数字缩放所有输入不会改变答案。让我们利用这一点设定 z = 1：

x³ + y³ = 4

任何这个两变量方程的有理数 x 和 y 解都可以缩放成原始三变量方程的整数解：(ax, ay, a)。我们还把 4 移到了左边，这会使我们后面的工作更方便。

现在，让我们乘以分母，使整个方程成为纯多项式：

x³ + y³ - 4 = 0

这引入了一些无关的解，例如 (0, 0)。但我们只需忽略它们。我们可以将上面的表达式绘制为函数；它看起来像这样：

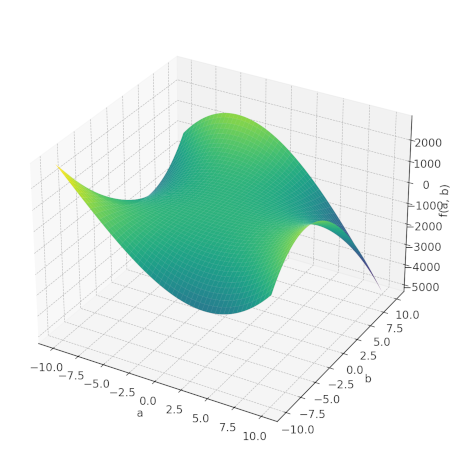
现在，让我们通过我们知道这条曲线与平面相交的两个点画一条线：(1, 1) 和 (4, -3)。我们通过从三值方程的两个解开始，并转换 z = 1 来推导这些点。

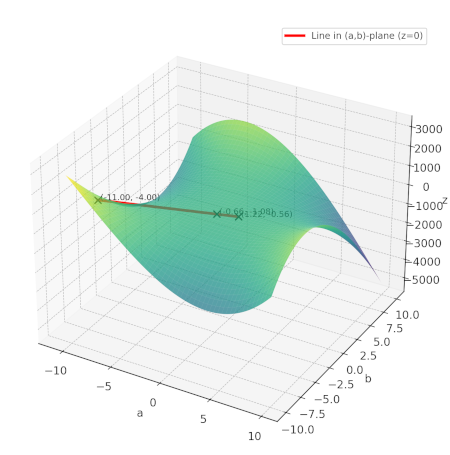
正如我们所见，这条线有第三个交点。因为这条线在平面上，第三个点也必须在平面上，因此它也必须是一个解。现在，让我们证明这个点是有理数，所以它仍然对应于原始问题的有效解。

我们可以将线参数化为 (x, y) = (1, 1) + t·(3, -4)。t = 0 给出第一个点，t = 1 给出第二个点。然后，我们可以通过将 x 和 y 替换为基于 t 的表达式来查看 f(x, y) 在线上的行为。

这给我们提供了曲线：f(t) = (1 + 3t)³ + (1 - 4t)³ - 4。这是该曲线的图，显示了所有三个交点：

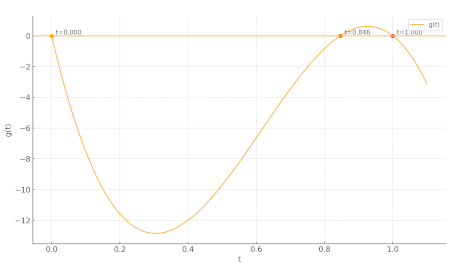
然后你可以将新的 t 代入线并得到你的新点：(x, y) = (1, 1) + t·(3, -4)。

新的 t（因此新的点）是有理数的基本原因是：曲线是 t 的三次多项式，如果一个三次多项式有三个解，那么它完全分解为 (t-t₁)(t-t₂)(t-t₃)。这个式子的二次项等于 -(t₁+t₂+t₃)。因此，如果二次项和三次项是有理数（它们确实是，因为我们用有理系数的方程构造了多项式），并且两个解是有理数，那么第三个解也必须是有理数。

从这里，我们可以通过暴力方法获得更多解。不幸的是，我们不能直接继续使用我们现有的三个点：如果你要重复上述过程，从我们现在拥有的三个点中的任意两个开始生成新点，你只会得到第三个点。为了克服这一点，我们将使用一个巧妙的技巧来生成更多的解：将 (x, y) 转换为 (y, x)。

现在，考虑到这一点，我们只需暴力计算，反复使用"找到线上的第三个点"算法和坐标翻转来获得尽可能多的新解。这是 Python 代码：

from sympy import symbols, Poly, solve, simplify, Rational, expand
from math import lcm

def find_third_point(a1, b1, a2, b2):
    """
    Find the third intersection point of a line through points (a1, b1) and (a2, b2)
    on the cubic curve a(a+1)(a+b) + b(b+1)(a+b) + (a+1)(b+1) = 4(a+1)(b+1)(a+b).
    
    Args:
        a1, b1: Coordinates of the first point (rational numbers)
        a2, b2: Coordinates of the second point (rational numbers)
    
    Returns:
        Tuple (a3, b3): Coordinates of the third intersection point
    """
    # Define symbolic variables
    t, a, b = symbols('t a b')
    
    # Parameterize the line: a = a1 + t*(a2 - a1), b = b1 + t*(b2 - b1)
    a_expr = a1 + t * (a2 - a1)
    b_expr = b1 + t * (b2 - b1)
    
    # Define the cubic curve equation:
    # a(a+1)(a+b) + b(b+1)(a+b) + (a+1)(b+1) = 4(a+1)(b+1)(a+b)
    left_side = a * (a + 1) * (a + b) + b * (b + 1) * (a + b) + (a + 1) * (b + 1)
    right_side = 4 * (a + 1) * (b + 1) * (a + b)
    equation = left_side - right_side
    
    # Substitute the line parameterization into the equation
    poly_t = equation.subs({a: a_expr, b: b_expr})
    
    # Simplify and convert to a polynomial in t
    poly_t = expand(poly_t)
    poly = Poly(poly_t, t)
    
    # Get the coefficients of the cubic polynomial
    coeffs = poly.coeffs()
    
    # The polynomial is cubic (degree 3), so coeffs = [c3, c2, c1, c0]
    # For a cubic c3*t3 + c2*t2 + c1*t + c0, the sum of roots is -c2/c3
    while len(coeffs) < 4:
        coeffs.append(0)
    if len(coeffs) != 4:
        raise ValueError("Unexpected polynomial degree. Expected cubic polynomial.")
    
    c3, c2, c1, c0 = coeffs
    
    # The known roots are t=0 (for point 1) and t=1 (for point 2)
    # Sum of roots: t1 + t2 + t3 = -c2/c3
    # Since t1 = 0, t2 = 1, we have 0 + 1 + t3 = -c2/c3
    t3 = -c2 / c3 - (0 + 1)
    
    # Compute the third point coordinates
    a3 = a1 + t3 * (a2 - a1)
    b3 = b1 + t3 * (b2 - b1)
    
    # Simplify the results to ensure rational output
    a3 = simplify(a3)
    b3 = simplify(b3)
    
    return (a3, b3)

# Verify the a point is on the curve
def is_on_curve(a, b):
    left = a * (a + 1) * (a + b) + b * (b + 1) * (a + b) + (a + 1) * (b + 1)
    right = 4 * (a + 1) * (b + 1) * (a + b)
    return left == right

def is_too_big(x, y):
    xn, xd = x.as_numer_denom()
    yn, yd = y.as_numer_denom()
    return max(abs(xn), abs(xd), abs(yn), abs(yd)) > 10**200

def find_smallest_all_positive_point():
    points = [(Rational(-11, 1), Rational(-4, 1)), (Rational(11, 9), Rational(-5, 9))]
    queue = [(points[0], points[1])]

    def accept(x, y):
        print(x, y)
        for (x2, y2) in points:
            queue.append(((x2, y2), (x,y)))
        points.append((x, y))

    while len(queue) > 0:
        print(len(queue))
        (x1, y1), (x2, y2) = queue.pop()
        x3, y3 = find_third_point(x1, y1, x2, y2)
        if not is_too_big(x3, y3):
            if (x3, y3) not in points:
                accept(x3, y3)
            if (y3, x3) not in points:
                accept(y3, x3)

    print(points)
    eligible = [(x,y) for (x,y) in points if x > 0 and y > 0]
    return min(
        eligible,
        key=lambda x: lcm(x[0].as_numer_denom()[1], x[1].as_numer_denom()[1])
    )

这非常低效，但它完成了任务。我们得到：

(154476802108746166441951315019919837485664325669565431700026634898253202035277999/4373612677928697257861252602371390152816537558161613618621437993378423467772036, 36875131794129999827197811565225474825492979968971970996283137471637224634055579/4373612677928697257861252602371390152816537558161613618621437993378423467772036)

这是两方程公式的正有理解；加上 z = 1，你得到三方程公式的正有理解。从这里，我们乘以分母，得到原始解。

a = 154476802108746166441951315019919837485664325669565431700026634898253202035277999 b = 36875131794129999827197811565225474825492979968971970996283137471637224634055579 c = 4373612677928697257861252602371390152816537558161613618621437993378423467772036

这并不证明这是最小的解：要证明这一点，你实际上需要深入到我努力避开的更深层次的椭圆曲线理论中。但它给你提供了一个问题的解决方案，而且背后的数学实际上是隐藏在其他形式中的椭圆曲线数学："找到线上的第三个交点并翻转坐标"与椭圆曲线加法法则完全相同，只是在对角轴上翻转而不是在x轴上翻转。我们得出的这种"加法法则"甚至满足结合律。