探索 circle STARK
作者:维塔利克·布特林 2024 年 7 月 23 日 原文链接
本文假设读者已熟悉 SNARK 和 STARK 的基本工作原理;如果您不熟悉,我建议阅读本文的前几个部分。特别感谢来自 Starkware 的 Eli ben-Sasson、Shahar Papini、Avihu Levy 和其他人的反馈和讨论。
过去两年 STARK 协议设计中最重要的趋势是转向使用小域。最早的 STARK 生产实现是在 256 位域上工作的——对大数如21888...95617进行模运算——这使得这些协议自然地兼容基于椭圆曲线的签名验证,并且易于推理。但这导致了效率低下:在大多数情况下,我们实际上没有很好的方法来利用这些较大的数字,所以它们最终大多是浪费的空间,甚至浪费了更多的计算,因为对 4 倍大的数字进行算术运算需要大约 9 倍的计算时间。为了解决这个问题,STARK 开始在更小的域上工作:首先是Goldilocks(模数)然后是Mersenne31 和 BabyBear(分别是和)。
这一转变已经带来了验证速度方面的显著提升,其中最引人注目的是 Starkware 能够在 M3 笔记本电脑上每秒验证 62 万个 Poseidon2 哈希。特别值得一提的是,如果我们愿意信任 Poseidon2 作为哈希函数,那么构建高效ZK-EVM最困难的部分之一实际上已经得到解决。但这些技术究竟是如何运作的呢?那些通常需要大数来保证安全性的加密证明,又是如何在这些域上构建的呢?与此同时,这些协议与更多奇特的构造(如这里所述)和Binius相比又如何呢?本文将探讨其中的一些细微差别,特别关注一个称为Circle STARKs的构造(该构造已在 Starkware 的stwo、Polygon 的plonky3和我用(某种)python 实现的版本中实现),它具有一些独特的特性,专门设计用于与高效的 Mersenne31 域兼容。
小域常见的问题
在制作基于哈希的证明(或实际上任何类型的证明)时,最重要的"技巧"之一是通过在随机点上评估多项式来证明特定性质,作为证明底层多项式的替代方法。
例如,假设一个证明系统要求你对一个多项式生成承诺,该多项式必须满足(这是 ZK-SNARK 协议中一个相当常见的证明类型)。协议可以要求你选择一个随机坐标,并证明。接着,为了证明,你需要证明是一个多项式(而不是分式表达式)。
如果你提前知道,你总是可以欺骗这些协议。在这种情况下,你可以直接将设为零,调整以满足方程,然后让成为通过这两点的直线。同样地,对于第二步,如果你提前知道,你可以生成任何你想要的内容,然后调整使其匹配,即使是分式(或其他非多项式)表达式。
为了防止这些攻击,我们需要在攻击者提供之后才选择("Fiat-Shamir 启发式"是将设置为的哈希值的专业术语)。重要的是,我们需要从一个足够大的集合中选择,使得攻击者无法猜到它。
在基于椭圆曲线的协议和 2019 年的 STARK 中,这很简单:我们所有的数学运算都是在 256 位数字上进行的,所以我们选择一个随机的 256 位数字作为,这就足够了。但在使用较小域的 STARK 中,我们遇到了一个问题:只有大约二十亿个可能的值可供选择,因此想要制作假证明的攻击者只需尝试二十亿次——这虽然工作量很大,但对于一个意志坚定的攻击者来说是完全可行的!
这个问题有两个自然的解决方案:
- 进行多次随机检查
- 扩展域
执行多次随机检查的方法直观且简单:与其在一个坐标上检查,不如在四个随机坐标上重复检查。理论上这是可行的,但存在效率问题。如果你处理的是在大小为 q 的域上的度数小于 d 的多项式,攻击者实际上可以构造出在 k 个位置上"看起来"良好的错误多项式。因此,他们在一轮协议中破坏的概率是 d/q。例如,如果 d=256 且 q=2031,这意味着攻击者每轮只能获得七位的安全性,所以你需要进行不是四轮,而是大约 18 轮检查,才能有效地防范此类攻击者。理想情况下,我们希望做 k 倍的工作,但只需要从安全级别中减去一次。
这就引出了另一个解决方案:扩展域。扩展域类似于复数,但是应用在有限域上:我们构想出一个新的值,称之为α,并声明α²=-1。乘法变成了:(a+bα)(c+dα)=(ac-bd)+(ad+bc)α。我们现在可以对数值对进行运算,而不仅仅是单个数字。假设我们在像 Mersenne 或 BabyBear 这样大小为 q 的域上工作,这使我们可以从 q²个值中选择 r。要达到更高的值,我们再次应用相同的技术,但由于我们已经使用了α,所以我们需要以不同方式定义一个新值:在 Mersenne31 中,我们选择β,其中β²=α。乘法现在变成
好吧,这是代码实现。它并不是最优的(你可以用Karatsuba 算法改进它),但它展示了基本原理。
现在,我们有了可供选择的值,这对于我们的安全需求来说已经足够高了:如果我们处理的是度数 < 的多项式,一轮就能获得 104 比特的安全性。如果我们想要更谨慎,达到更广泛接受的 128 比特安全级别,我们可以在协议中加入一些工作量证明(proof of work)。
请注意,我们实际上只在 FRI 协议中使用这个扩展域(extension field),以及其他需要随机线性组合的情况。大部分数学运算仅在"基础域"(base field,模或)中完成,几乎所有被哈希的数据都在基础域中,所以每个值只需要哈希四个字节。这让我们既能受益于小域的效率,又能在需要时利用更大的域来保证安全性。
常规 FRI
在构建 SNARK 或 STARK 时,第一步通常是算术化:将任意计算问题简化为一个方程,其中一些变量和系数是多项式(例如,方程通常看起来像某种形式,其中、和是已知的,求解者需要提供和)。一旦你有了这样的方程,方程的解就对应着底层计算问题的解。
为了证明你有一个解,你需要证明你所提出的值实际上是真实的多项式(而不是分数,或在一个地方看起来像一个多项式而在另一个地方看起来像不同多项式的数据集,或者其他情况),并且具有特定的最大次数。为了做到这一点,我们迭代地应用随机线性组合技巧:
- 假设你有一个多项式的求值,你想证明它的次数是某个值
- 考虑多项式、和
- 令为一个随机线性组合
本质上,这个过程是这样的:分离了的偶数系数,而分离了奇数系数。给定和,你可以通过公式恢复:。而如果真的具有特定次数,那么(i)和的次数为。并且作为一个随机线性组合,的次数也必须为相同值。
我们已经将一个"证明次数"问题简化为另一个"证明次数"问题。重复这个过程 20 次,你就得到了一个被称为"快速里德 - 所罗门交互式预言机近似证明"(简称"FRI")的技术。如果有人试图通过这个技术推送一个不是次数多项式的内容,那么第二轮的输出将(以一定概率)不会是次数多项式,第三轮的输出也不会是次数多项式,以此类推,最终的检查将会失败。在大多数位置等于次数多项式的数据集虽然有一定概率通过该方案,但要构造这样的数据集,你需要知道底层的多项式,因此即使这样一个略有缺陷的证明也能令人信服地表明证明者如果愿意的话可以生成一个"真实的"证明。在证明这对所有可能的输入都成立时还存在更多技术复杂性;理解这些细节一直是过去五年学术 STARK 研究的主要焦点。
让我们更详细地了解这里发生的事情,以及使这一切运作所需的属性。在每一步中,我们都将次数减少 2 倍,同时也将定义域(我们观察的点集)减少 2 倍。前者是使 FRI 能够运作的关键,而后者则使其变得如此快速:因为每一轮都比前一轮小 2 倍,总成本变成了而不是。
为了实现这种定义域的缩减,我们需要一个二对一映射:。这个二对一映射的优点在于它是可重复的:如果你从一个乘法子群(一个集合)开始,那么你就从一个集合开始,其中对于集合中的任何,也在集合中(如果,)。如果你然后对其求平方得到,那么完全相同的性质依然适用,因此你可以一直减少到只剩一个值(尽管在实践中我们通常会稍早停止)。
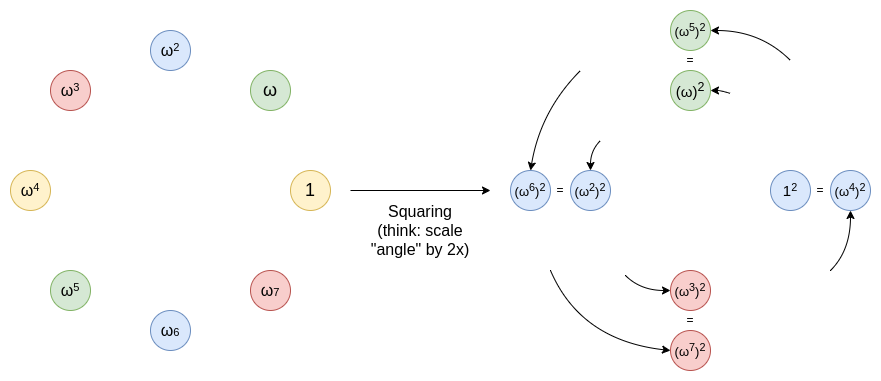
你可以将其想象成一条环绕圆周的线,然后将这条线拉伸至绕圆两周的操作。在 x 度的点会变成 2x 度的点。从 0 到 179 度的每个点都会与 180 到 359 度之间的对应点重叠。这个过程可以不断重复。
要实现这一点,你需要原始的乘法子群的大小包含较大的 2 的幂作为因子。BabyBear 的模数为,因此最大可能的子群是所有非零值——即大小为。这非常适合上述技术。你可以使用大小为的子群,或者直接使用完整集合,通过 FRI 将多项式降至 15 次,然后在最后直接检查次数。然而,Mersenne31 并不能这样工作。其模数为,因此乘法子群的大小为。这只能被 2 除一次。从那之后,我们就无法进行 FFT 了——至少不能使用上述技术。
这是一个遗憾,因为 Mersenne31 是一个超级方便的用于现有 32 位 CPU/GPU 运算的域。如果你将两个数相加,结果可能超过,但你可以通过计算来降低它,其中是位移。对于乘法,你可以做类似的操作,不过你需要使用一个特殊(但常见)的操作码,它返回乘法结果的"高位"(即)。这使得算术运算效率比 BabyBear 高约 1.3 倍。如果我们能够在 Mersenne31 上进行 FRI,这将使情况显著改善。
Circle FRI
这就是circle STARKs的巧妙之处。给定一个素数,我们可以轻松获得一个具有类似二对一特性的大小为的群:点集满足。让我们来看看模 31 下的这个结构: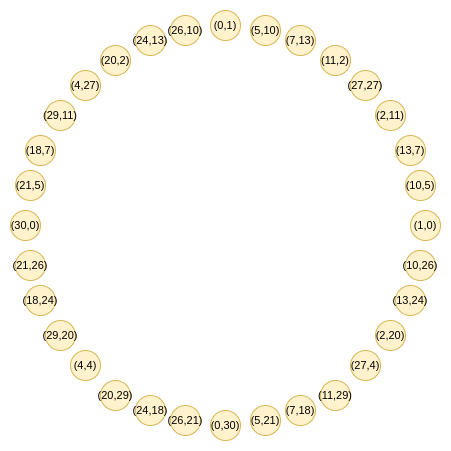
这些点遵循一个加法规则,如果你最近学习过三角函数或复数乘法,这个规则会让你感到很熟悉:
二倍形式是:
现在,让我们只关注这个圆上"奇数"位置的点: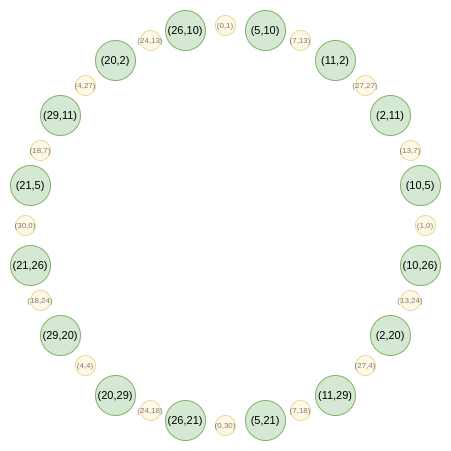
这就是我们的 FFT。首先,我们将所有点压缩到一条线上。我们在常规 FRI 中使用的和公式的等价形式是:
然后,我们可以取一个随机线性组合,得到一个在 x 轴子集上的一维: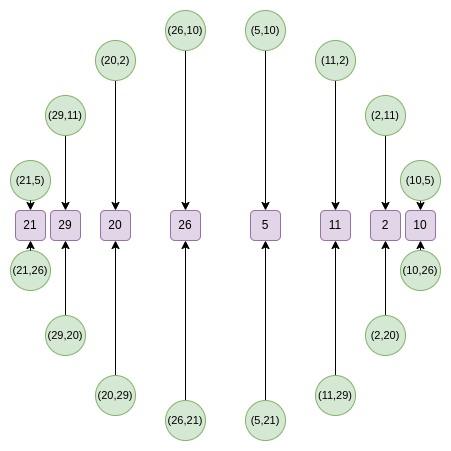
从第二轮开始,映射发生变化:
这个映射实际上每次都会将上述集合的大小减半!这里发生的事情是,每个点在某种意义上都"代表"两个点:和。而是上面提到的点倍乘法则。因此,我们取圆上两个相对点的坐标,并将其转换为倍乘点的坐标。
例如,如果我们取从右边数第二个值,,并应用映射,我们得到。如果我们回到原始圆,是从右边逆时针数第三个点,所以如果我们将其加倍,就会得到从右边逆时针数第六个点,也就是...。
这些操作本可以全部在二维上完成,但在一维上操作会使事情变得更加高效。
Circle FFTs
与 FRI 密切相关的一个算法是快速傅里叶变换,它可以将多项式的一组求值结果转换为该多项式的系数。FFT 遵循与 FRI 相同的路径,但不同之处在于,它不是在每一步生成随机线性组合,而是递归地对两部分分别应用规模减半的 FFT,然后将输出作为偶数系数和奇数系数。
圆群也支持 FFT,它也是按照类似的方式从 FRI 构建的。然而,circle FFTs(和 circle FRI)所处理的对象在技术上并不是多项式,这是一个关键的区别。相反,它们是数学家所说的黎曼 - 罗赫空间:在这种情况下,是关于圆()取模的多项式。也就是说,我们将任何的倍数都视为零。另一种理解方式是:我们只允许的一次幂:一旦出现项,就将其替换为。
这还暗示了另一件事:circle FFT 输出的"系数"不像常规 FRI 中的单项式那样(例如,如果常规 FRI 输出,那么我们知道这表示)。相反,这些系数是在一个特定于 circle FFTs 的特殊基底中:
好消息是,作为开发者,你几乎可以完全忽略这一点。STARKs 不会要求你了解这些系数。相反,你可以始终将"多项式"以特定域上的一组求值形式存储。你唯一需要使用 FFT 的地方,是在执行(黎曼 - 罗赫空间意义下的)低次扩展时:即给定个值,生成在同一多项式上的个值。在这种情况下,你可以通过 FFT 生成系数,在这些系数后附加零,然后通过逆 FFT 来获得更大的求值集。
圆周 FFT(快速傅里叶变换)并不是唯一一种"特殊 FFT"。椭圆曲线 FFT更为强大,因为它们可以在任何有限域(素数域、二进制域等)上运行。然而,ECFFT 更难理解且效率较低,因此我们仍然使用圆周 FFT。 接下来,让我们深入探讨一些更深奥的细节,这些细节对于实现圆周 STARK 的人来说,与常规 STARK 相比会有所不同。
商运算(Quotienting)
在 STARK 协议中,一个常见的操作是在特定点(无论是刻意选择的还是随机选择的)进行商运算。例如,如果你想证明,你需要提供,并证明是一个多项式(而不是分数值)。随机选择评估点在 DEEP-FRI 协议中得到应用,这使得 FRI 在使用更少的默克尔分支的情况下也能保持安全性。
在这里,我们遇到了一个微妙的挑战:在圆群中,不存在类似于常规 FRI 中的那种只经过一个点的线性函数。从几何角度可以看出这一点: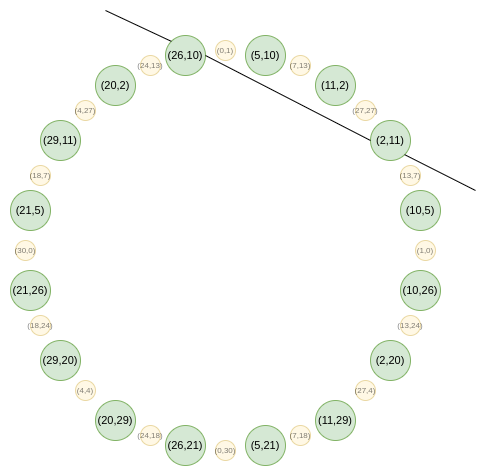
你可以构造一个在某点切于圆的线性函数,但这条线会以"二重"的方式经过该点。也就是说,要使一个多项式成为该线性函数的倍数,它必须满足比仅在该点为零更严格的条件。因此,你无法仅证明一个点的取值。那么我们该怎么办呢?基本上,我们只能接受现实,转而证明两个点的取值,添加一个我们不需要关心其取值的虚拟点。
一个线性函数:。如果你通过令其等于 0 将其转换为方程,你可能会认出这就是高中数学中所说的"标准形式"中的直线。
如果我们有一个多项式在点取值为,在点取值为,那么我们选择一个插值函数:一个在点取值为,在点取值为的线性函数。这可以简单到。然后我们通过减去(这样在两点处都等于零),除以(和两点之间的线性函数),并证明商是一个多项式,来证明在和两点处分别等于和。
消失多项式
在 STARK 中,你试图证明的多项式方程通常看起来像这样,其中是一个在整个原始求值域上等于零的多项式。在"常规"STARK 中,该函数就是。在圆形 STARK 中,等价的是:
请注意,你可以从折叠函数中推导出消失多项式:在常规 STARK 中,你在重复运算,在这里你也在重复运算,不过对于第一轮你做的事情不同,因为第一轮是特殊的。
比特位反转顺序(Reverse bit order)
在 STARK 中,多项式的求值通常不按"自然"顺序排列(,,...),而是按照我称之为"比特位反转顺序"的方式:
,,,,,,,,...
如果我们设定,并且我们只关注我们在哪些幂次上求值,列表看起来是这样的:
这种排序具有一个关键特性:在 FRI 求值的早期阶段被分组在一起的值,在排序中会被放在彼此相邻的位置。例如,FRI 的第一步将和分组在一起。在这种情况下,,所以这意味着和。正如我们所看到的,这些正好是相邻的成对值。FRI 的第二步将,,和分组在一起。这些正好是我们看到的四个一组的分组。依此类推。这使得 FRI 的空间效率更高,因为它允许你为被折叠在一起的两个值(或者如果你一次折叠多轮,则为所有值)同时提供一个 Merkle 证明。
在圆形 STARK 中,折叠结构略有不同:在第一步中,我们将与组合在一起,在第二步中与组合,在后续步骤中与组合,选择和使得,其中是重复次的映射。如果我们从圆周上的位置来考虑这些点,在每一步中,这看起来就像是第一个点与最后一个点配对,第二个点与倒数第二个点配对,以此类推。
为了调整比特位反转顺序以反映这种折叠结构,我们反转除最后一位之外的每一位。我们保留最后一位,并且也用它来决定是否翻转其他位。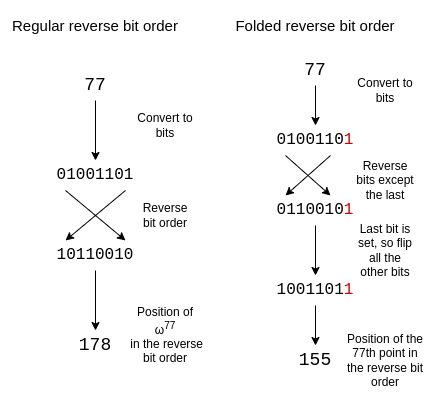
大小为 16 的折叠比特位反转顺序如下所示:
如果你看上一节中的圆,第 0、15、8 和 7 个点(从右侧开始逆时针方向)的形式为,,和,这正是我们所需要的。
效率
Circle STARK(以及一般的 31 位素数 STARK)非常高效。在 Circle STARK 中被证明的实际计算很可能涉及几种类型的计算:
效率的关键衡量标准是:你是否在计算轨迹中充分利用了所有空间来进行有用的工作,还是留下了大量浪费的空间?在大域 SNARK 中,存在大量浪费的空间:业务逻辑和查找表主要涉及小数字的计算(通常在 N 步计算中,数字都小于 N,所以在实践中较小),但你仍然要承担使用 -比特域的成本。在这里,域的大小为,所以浪费的空间并不大。"为 SNARK 设计"的低算术复杂度哈希(例如 Poseidon)在任何域中都充分利用了轨迹中每个数字的每一位。
因此,Circle STARK 实际上非常接近最优!Binius 甚至更强大,因为它允许你混合搭配不同大小的域,从而为所有运算实现更高效的位打包。Binius 还为实现 32 位加法提供了选项,无需承担查找表的开销。然而,这些收益是以(在我看来)显著增加理论复杂性为代价的,相比之下,Circle STARK(更不用说基于 BabyBear 的常规 STARK)在概念上相当简单。
结论:我如何看待环形 STARK?
与常规 STARK 相比,环形 STARK 并没有给开发者带来太多额外的复杂性。在实现过程中,与常规 FRI 相比,上述三个问题实际上是我看到的唯一的区别。环形 FRI 所操作的"多项式"背后的基础数学确实比较反直觉,需要一定时间才能理解和领会。但恰好这种复杂性被很好地隐藏起来,对开发者来说并不那么明显。环形数学的复杂性是被封装的,而不是系统性的。
理解环形 FRI 和环形 FFT 也可以作为理解其他"特殊 FFT"的良好思维入门:最值得注意的是二进制域 FFT,它被用于 Binius 以及此前的 LibSTARK,还有一些更深奥的构造,比如椭圆曲线 FFT,它们使用了与椭圆曲线点运算配合良好的少对一映射。
结合 Mersenne31、BabyBear 和像 Binius 这样的二进制域技术,感觉我们正在接近 STARK "基础层"效率的极限。在这一点上,我预计 STARK 优化的前沿将转向为哈希函数和签名等基本组件制作最高效的算术化(并为此目的优化这些基本组件本身)、构建递归结构以实现更多并行化、虚拟机的算术化以改善开发者体验,以及其他更高层次的任务。
