ETHStudy

以太坊协议的可能未来 ❹：Verge ​

作者：维塔利克·布特林 2024年10月23日 原文链接

区块链最强大的地方之一在于，任何人都可以在自己的电脑上运行一个节点，并验证链的正确性。即使运行链共识(PoW、PoS等)的95%的节点立即同意更改规则并开始根据新规则生产区块，运行完整验证节点的人也可以拒绝接受这条链。没有参与这一共谋的质押者仍可以继续构建遵循旧规则的链条，而运行全验证（fully-verifying）的用户也可沿着这条链前行。

这是区块链与中心化系统的一个关键区别。然而，为了保持这一特性，必须能让很多人可以运行全验证节点。这同时适用于质押者(如果质押者没有验证链条，他们实际上并未为执行协议规则做出贡献)和普通用户。现在，在消费级笔记本电脑上运行节点是可能的(包括用于撰写这篇文章的电脑)，但这样做困难重重。The Verge 的目的是改变这种状况，使验证整条链的计算成本低廉到每个移动钱包、浏览器钱包，甚至智能手表都可以默认执行此操作。

特别感谢Justin Drake、Hsiao-wei Wang、Guillaume Ballet、Ignacio、Josh Rudolf、Lev Soukhanov、Ryan Sean Adams和Uma Roy的反馈与审阅。

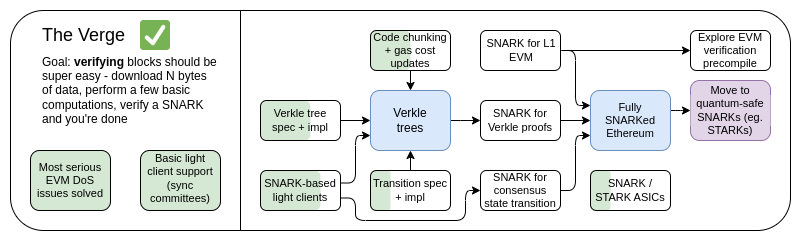The Verge ，2023年路线图

最初，The Verge 是指，将以太坊状态存储迁移到 Verkle树的想法——一种树状结构，可以生成更紧凑的证明，从而实现无状态验证以太坊块。节点可以验证以太坊块而无需在硬盘上存储任何以太坊状态(账户余额、合约代码、存储等)，代价是需要花费几百KB的证明数据和几百毫秒来验证证明。如今，The Verge 代表了一个更广阔的愿景，专注于实现对以太坊链进行最大程度资源高效的验证，其中不仅包括无状态验证技术，还包括使用SNARK验证所有以太坊执行。

SNARK / STARK

  • SNARK, succinct non-interactive argument of knowledge，简洁非交互式知识证明
  • STARK，scalable transparent argument of knowledge，可扩展透明知识证明

除了增加对使用SNARK验证整条链的长期关注外，另一个新问题在于Verkle树是否真的是最佳技术选择。Verkle树对量子计算机是脆弱的，因此如果我们用Verkle树取代当前的KECCAKMerkle Patricia树，我们将不得不再次替换这些树。Merkle树的自然替代方案是直接跳到使用STARK 的二叉树 Merkle分支。历史上，由于开销和技术复杂性，这被认为是不可行的。然而，最近我们看到Polygon在笔记本电脑上以每秒1.7百万个Poseidon哈希证明使用circle STARK，而对于更"传统"的哈希函数，由于技术如GKR，证明时间也在迅速缩短。

因此，在过去一年中，The Verge 变得更加开放，有几种可能的发展路径。

说明

为 Vitalik 文章的全文翻译，为便于阅读增加少量标签式图示展示重要术语。

The Verge：关键目标 ​

  • 无状态客户端：完全验证客户端和股权证明节点不应需要超过几GB的存储空间
  • (长期目标)在智能手表上完全验证链(共识和执行)。下载一些数据，验证一个SNARK(简洁非交互式知识证明)，就完成了。

本章内容 ​

  • 无状态验证：Verkle树或STARK
  • EVM执行的正确性证明
  • 共识的正确性证明

无状态验证：Verkle树或STARK ​

我们试图解决什么问题? ​

如今，以太坊客户端需要存储数百GB的状态数据才能验证区块，而这一数量还在不断增加。原始状态数据每年增长约30GB，个人客户端还需要存储一些额外数据，以便能够高效地更新Merkle树。

这降低了可以运行完全验证以太坊节点的用户数量：尽管可以轻松购买到足以存储所有以太坊状态数据及多年历史数据的大容量硬盘，但普通用户购买的计算机通常只有几百GB的存储空间。状态数据的大小也给首次设置节点带来了很大阻力：节点需要下载整个状态数据，这可能需要数小时甚至数天的时间。这产生了各种连锁反应。例如，它使得为质押者升级质押设置变得非常困难。从技术上讲，这是可以实现无停机升级的——启动新客户端，等待其同步，再关闭旧客户端并转移密钥——但在实践中，这个过程在技术上相当复杂。

它是什么？工作原理是什么？ ​

无状态验证是一种技术，允许节点在不存储整个状态数据的情况下进行区块验证。相反，每个区块都附带一个见证(witness)，其中包括(i)区块将访问的特定状态位置的值(如代码、余额、存储)，以及(ii)这些值正确性的加密证明。

实际实现无状态验证需要改变以太坊状态树的结构。这是因为当前的Merkle Patricia树(MPT)对于实现任何加密证明方案都非常不友好，尤其是在最坏情况下。无论是"原始"Merkle分支，还是将Merkle分支封装在STARK中的可能性，MPT存在的两个主要弱点都会带来困难：

  1. 它是一棵16叉树(即每个节点有16个子节点)。这意味着在大小为N的树中，平均一个证明需要 32 * (16 - 1) * log16(N) = 120 * log2(N) 字节，或在2^32项的树中约3840字节。而对于二叉树，你只需 32 * (2 - 1) * log2(N) = 32 * log2(N) 字节，或在一棵2^32项的树中约1024字节。
  2. 代码没有Merkle化。这意味着证明任何对账户代码的访问都需要提供整个代码，最多可达24000字节。

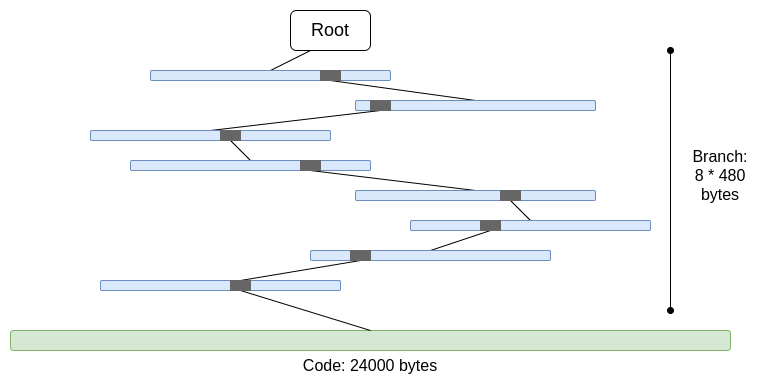
我们可以计算出最坏情况下的数据量：

30,000,000 gas / 2,400 (冷账户读取成本) * (5 * 480 + 24,000) = 330,000,000 字节

由于当有大量分支时，分支顶部的部分是重复的，因此分支成本略有降低(5 * 480 而非 8 * 480)。但即便如此，在一个时隙内需要下载330MB的数据，这在现实中是完全不可行的。如果我们尝试用STARK封装它，则会遇到两个问题：(i)KECCAK相对而言不太适合STARK，(ii)330MB的数据意味着我们需要证明对KECCAK轮函数进行500万次调用，这远远超出了普通消费级硬件的能力，即使我们能够大幅提高STARK证明KECCAK的效率。

如果我们将16叉树替换为二叉树，并且对代码进行Merkle化，那么最坏情况下的数据量大约为30,000,000 / 2,400 * 32 * (32 - 14 + 8) = 10,400,000字节(其中14是约2^14个分支的冗余比特数，8是进入一个chunk叶子的证明长度)。注意，这需要调整gas成本，以收取访问每个单独代码chunk的费用；EIP-4762就是这样做的。10.4MB虽然好多了，但对于许多节点在一个时隙内下载仍然太多。因此，我们需要引入更强大的技术。为此，有两种主要解决方案：Verkle树和基于STARK的二进制哈希树。

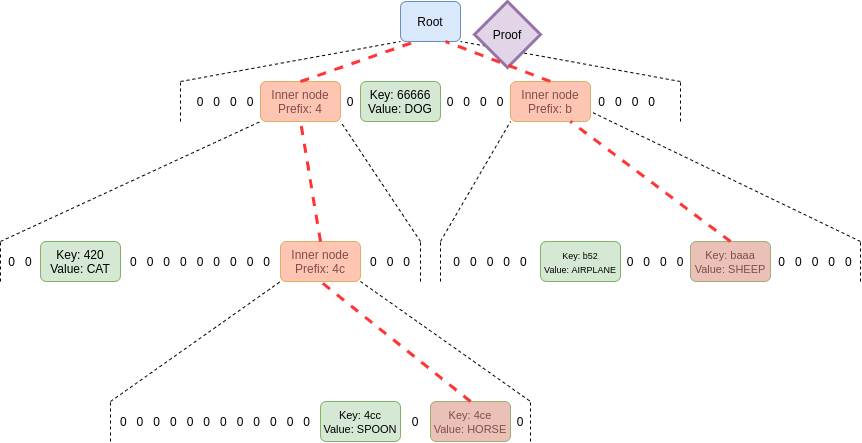
Verkle Tree

Verkle 树 ​

Verkle 树使用基于椭圆曲线的向量承诺来生成更短的证明。关键是与每个父子关系相对应的证明部分仅为32字节，而与树的宽度无关。树的宽度唯一的限制是，如果树过于宽阔，证明会在计算上效率低下。为以太坊提出的实现具有256的宽度。

因此，单个分支中的证明大小为32 * log256(N) = 4 * log2(N)字节。理论上最大的证明大小因此大约为30,000,000 / 2,400 * 32 * (32 - 14 + 8) / 8 = 1,300,000字节(实际计算方式由于状态块分布不均略有不同，但作为初步估计是可以的)。

需要注意的是，在所有上述示例中，这个"最坏情况"并不完全是最糟糕的情况：更糟糕的情况是攻击者蓄意构造两个地址，使其在树中具有较长的公共前缀，并从其中一个地址读取数据，这可能会使最坏分支长度再延长约2倍。但即使考虑这一点，Verkle 树也将最糟糕的证明大小控制在约2.6 MB左右，大致与当前最糟糕的calldata相当。

我们还利用这一点做了另一件事：我们使访问"相邻"存储变得非常便宜，无论是同一合约的多个代码块，还是相邻的存储槽。EIP-4762对相邻性进行了定义，并且只需支付200 gas即可访问相邻存储。对于相邻访问，最坏情况下的证明大小变为30,000,000 / 200 * 32 = 4,800,800字节，仍在可接受范围内。如果我们希望进一步降低这个值以增加安全性，我们可以适当提高相邻访问的gas成本。

STARK

使用 STARK 压缩 Merkle 树数据 ​

这项技术的思路很直白：对于需要证明区块中某些值的 Merkle 树状数据结构，生成最多 10.4MB 的证明数据，然后使用 STARK 对这个证明本身进行证明。通过这种方式，证明本身只包含被证明的数据，外加大约 100-300kB 的 STARK 固定开销。

这里的主要挑战在于 prover 的计算时间。我们可以做与上面大致相同的计算，只不过这次我们计算的是哈希值而不是字节数。以太坊当前区块大小限制为 10.4MB，意味着区块包含约 330,000 个哈希值。如果我们加上攻击者可能构造地址使其在 Merkle 树中具有较长公共前缀的可能性，真正的最坏情况会变为需要计算约 660,000 个哈希值。因此，如果 prover 在生成 STARK 证明时能够每秒处理约 200,000 个哈希值，就没问题了。

这些数字已经在消费级笔记本电脑上使用专为 STARK 友好性设计的 Poseidon 哈希函数达到了。然而，Poseidon 相对不太成熟，因此许多人还不太相信它的安全性。因此，目前有两条现实的发展路径：

  1. 尽快对 Poseidon 做大量安全性分析，并足够放心将其部署在以太坊主网(L1)上
  2. 使用更"保守"的哈希函数，如 SHA256 或 BLAKE

Starkware 的 circle STARK 证明器(一种特定的 STARK 证明系统实现)目前在消费级笔记本电脑上如果证明保守的哈希函数，每秒只能证明约 10-30k 次哈希运算。然而，STARK 技术发展迅速。即使在今天，基于 GKR 的技术也有望将此提高到 100-200k 的范围。

见证者除验证区块外的其他用例 ​

除了验证区块，更有效的零知识证明还有三个关键用例：

  • 内存池: 当交易被广播时，p2p网络中的节点需要先验证交易是否有效，才会重新广播。目前，验证包括核实签名、检查余额是否足够以及nonce是否正确。将来(例如，在采用原生账户抽象的情况下，如EIP-7701)，这可能需要运行一些EVM代码，对状态进行访问。如果节点是无状态的，交易将需要附带证明来证明相关状态对象。

  • 包含交易列表: 这是一个提议中的功能，允许(可能较小且不太先进的)权益证明验证者强制下一个区块包含某笔交易，而无需(可能大型且先进的)区块构建者同意。这将减少强大行为体操纵区块链延迟交易的能力。然而，这需要验证者有一种方法来验证包含交易列表中交易的有效性。

  • 轻客户端: 如果我们希望通过钱包(如Metamask、Rainbow、Rabby...)访问链的用户无需信任中心化参与者，他们需要运行轻客户端(如Helios)。核心Helios模块为用户提供经过验证的状态根哈希值。但为了完全可信，用户需要为每个单独的RPC调用获得证明(例如，对于eth_call请求，用户需要获得对所有在调用期间被访问的状态的证明)。

这些用例都共同的一点是需要相当多的证明，但每个证明本身都很小。因此，STARK证明实际上并不适用于它们；相反，直接使用Merkle证明分支更为实际。Merkle证明分支的另一个优点是可以进行更新：如果获得了状态对象X的证明，并且该证明是以区块B为根，那么如果之后收到了子区块B2及其见证数据，就可以将该证明更新为以区块B2为根。Verkle证明也天生具有可更新性。

查看更多：现有研究资料链接

现有研究资料链接 ​

待解决的问题及权衡考虑 ​

主要剩余的工作是：

  1. 更多关于EIP-4762 (静态性气体成本变更)影响的分析
  2. 完成并测试过渡程序，这是任何静态性EIP的一个复杂部分
  3. 更多对 Poseidon、Ajtai 和其他"STARK 友好"哈希函数的安全性分析
  4. 针对广泛使用且经过大量测试的"传统"哈希函数(如基于 Binius 或 GKR 的想法)的超高效 STARK 协议进行更多开发。

我们也将很快面临三种选择的决策点：(i) Verkle 树、(ii) STARK 友好哈希函数，以及(iii) 传统哈希函数。它们的特性可以大致总结在下表中：

算法证明数据大小安全假设当前最坏情况证明者时间
Verkle数据加~100-2,000 kB基于椭圆曲线(不抗量子攻击)< 1秒
基于传统哈希函数的STARK
(如SHA256、BLAKE)		数据加~100-300 kB传统广泛使用的哈希函数> 10秒
基于STARK友好哈希函数的STARK
(Poseidon、Ajtai)		数据加~100-300 kB相对较新且经过较少测试的哈希函数1-2秒

除了这些数字外，还有一些其他重要考虑因素：

  • 目前，Verkle树代码相当成熟。使用除Verkle以外的任何其他方案，在现实中都可能会延迟部署，可能需要推迟一次硬分叉。如果我们需要额外的时间来研究哈希函数分析或证明者实现，并且如果我们有其他重要功能希望更早纳入以太坊，那么这是可以接受的。

  • 与Verkle树相比，使用哈希更新状态根更快。这意味着基于哈希的方法可以降低完整节点的同步时间。

  • Verkle树具有有趣的证明更新属性 - Verkle树证明是可更新的。这一特性对于内存池、包含列表和其他用例很有用，它还可以潜在地帮助实现更高效：如果更新了状态对象，你可以在倒数第二层更新证明，而无需读取最后一层。

  • Verkle树证明更难用于SNARK证明。如果我们想将证明大小减小到几千字节，用Verkle证明会带来一些困难。这是因为验证Verkle证明需要大量256位操作，这就需要证明系统或者拥有大量开销，或者本身具有256位部分专门用于Verkle证明的内部构造。这对于无状态性本身并不是问题，但确实在以后引入了一些困难。

如果我们希望以量子安全且相当高效的方式获得Verkle证明可更新的特性，一种其他可能的途径是基于格网的Merkle树。

如果证明系统在最坏情况下效率不够，我们可以使用的另一个"应急方案"是多维 gas（multidimensional gas）:为(i) calldata、(ii) 计算、(iii) 状态访问等不同资源设置单独的gas限制。虽然多维 gas会增加复杂性，但作为交换，它可以更加严格限制平均情况和最坏情况之间的比率。使用多维 gas，理论上最大需要证明的分支数可能从30,000,000 / 2400 = 12,500下降到例如3000。这将使BLAKE3(勉强)在今天就足够了，即使没有进一步的证明者改进。

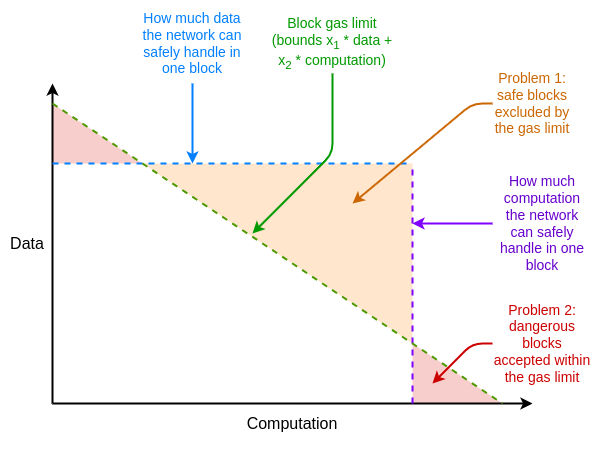
多维 gas可以使区块的资源限制更好地反映底层硬件资源的限制。

另一个出人意料的设计是这个提案，将状态根计算推迟到区块所在时隙之后。这将为我们提供整整12秒的时间来计算状态根，这意味着即使在最极端的情况下，仅需约60,000次哈希/秒的证明时间就足够了，再次使BLAKE3勉强满足需求。

这种方法的缺点是它将增加轻客户端的延迟时间为一个时隙，尽管有一些更加巧妙的技术变种可以将这种延迟减少到仅为证明生成延迟的时间。例如，证明可以在任何节点生成后立即在网络上广播，而不是等待下一个区块。

它与路线图其他部分的关系 ​

解决无状态验证问题可以极大地增加独立质押的便利性。如果出现了旨在降低独立质押最低余额要求的技术，如 Orbit SSF 或应用层策略(如squad staking)的话，此优势就更加可贵了。

如果引入以太坊改进提案EOF(EOF)，多维 gas就会变得更容易实现。这是因为多维 gas在执行过程中的一个关键复杂性是处理不传递父调用全部gas的子调用，而EOF通过简单地使此类子调用非法(并且本地账户抽象将为目前这种部分gas子调用的主要使用案例提供协议级替代方案)使得这个问题变得很简单。

另一个重要的协同效应是无状态验证和历史数据过期。现在，客户端必须存储近乎1TB的历史数据；这些数据比全状态数据大好几倍。即使客户端实现了无状态验证，也无法实现几乎无存储需求的梦想，除非我们能够解除客户端存储历史数据的责任。在这方面的第一步是EIP-4444，它也意味着将历史数据存储在种子或门户网络中。

EVM执行证明

以太坊虚拟机执行的有效性证明 ​

我们试图解决什么问题? ​

以太坊区块验证的长期目标是明确的：你应当能够通过 (i) 下载区块，或者甚至只下载区块的部分数据进行数据可用性采样，以及 (ii) 验证一个简洁的证明来证实该区块的有效性。这将是一个极低资源占用的操作，可在移动客户端、浏览器钱包中执行，甚至可在另一条链上执行(无需数据可用性部分)。

实现此目标需要对(i)共识层(即权益证明)和(ii)执行层(即以太坊虚拟机EVM)拥有 SNARK 或 STARK 证明。前者本身就是一项挑战，应在持续改进共识层的过程中(如实现单时隙确定性)解决。后者需要对以太坊虚拟机执行的证明。

它是什么？工作原理是什么？ ​

在以太坊规范中，以太坊虚拟机被正式定义为一个状态转换函数：你有一个预状态S、一个区块B，你正在计算一个后状态S' = STF(S， B)。如果用户使用轻客户端，他们没有完整的S、S'或B；相反，他们只有一个预状态根R、一个后状态根R'和一个区块哈希H。需要被证明的完整陈述大致如下：

  • 公共输入：预状态根R、后状态根R'、区块哈希H
  • 私有输入：区块主体B、区块访问的状态对象Q、执行区块后的相同对象Q'、状态证明(如Merkle分支)P
  • 声明1: P是Q中包含由R表示的某部分状态的有效证明
  • 声明2:如果你在Q上运行STF，(i)执行只访问Q内的对象，(ii)区块是有效的，并且(iii)结果是Q'
  • 声明3:如果你使用来自Q'和P的信息重新计算新的状态根，计算得到的结果将为R'

如果存在这种情况，你就可以拥有一个完全验证以太坊虚拟机执行的轻客户端。这已经允许客户端资源占用相当低。要实现真正的完全验证以太坊客户端，你还需要对共识方面做同样的事情。

查看更多：现有研究资料链接

现有研究资料链接 ​

待解决的问题及权衡考虑 ​

现有的EVM有效性证明在 安全性 和 证明器时间 两个方面都不够充分。

一个安全的有效性证明需要确保SNARK实际上验证了EVM计算，其中不存在任何bug。提高安全性的两种主要技术是多证明器和形式化验证。多证明器是指拥有多个独立编写的有效性证明实现，就像存在多个客户端一样，只要其中足够多的实现证明了某个区块，客户端就接受该区块。形式化验证则是使用诸如Lean4这样常用于证明数学定理的工具，证明某个有效性证明只接受符合底层EVM规范(例如EVM K语义或用Python编写的以太坊执行层规范(EELS))的输入。

证明器时间足够快，意味着任何以太坊区块都可在4秒内被证明。虽然我们离这个目标仍有一定距离，但比两年前想象的可能性要近得多。为达成这一目标，我们需要在三个方向上取得进展：

  • 并行化 - 目前最快的EVM证明器可以在约15秒内证明一个 平均 以太坊区块。它通过在数百个GPU之间并行计算，最后将结果合并而实现。理论上，我们确切知道如何构建一个能以O(log(N))时间证明计算的EVM证明器：让每个GPU处理一步，然后进行"汇总树"操作：

    虽然存在实现上的挑战。即使在最坏情况下(例如一个巨大的交易占据整个区块)，划分计算时也不能按交易划分，而必须按EVM或更底层VM(如RISC-V)的操作码划分。其中一个关键的实现挑战是，需要确保VM的"内存"在证明的不同部分间保持一致。然而，如果我们 能够 构建这种递归证明，那么至少在证明器延迟问题上就可以解决，即使在其他方面没有任何改进。

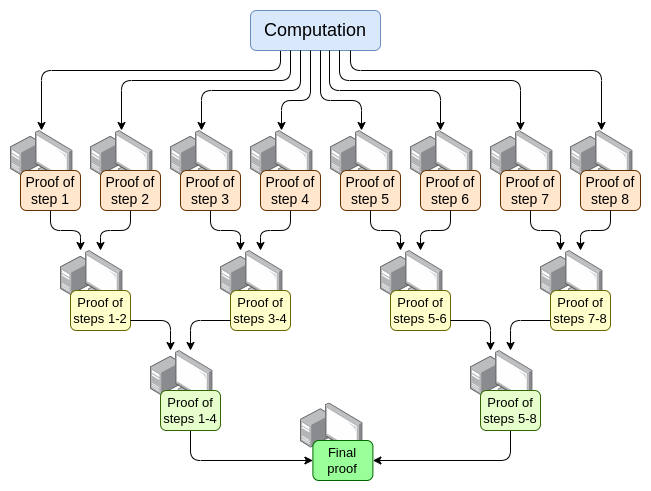
  • 优化证明系统 - 新的证明系统如Orion、Binius、GKR等，可能会进一步大幅减少通用计算的证明器时间。

  • 优化EVM gas成本等 - EVM中有许多部分可以进行优化，尤其是在 最坏情况下，使之对证明器更加友好。仅能在4秒内证明平均的以太坊区块是不够的，如果攻击者可以构造出需耗费证明器10分钟才能完成的区块。所需的EVM更改主要可归为两类：

    • 调整gas成本 - 如果某个操作耗费证明器大量时间，即使它实际计算很快，也应该设置高gas成本。EIP-7667就是一个拟调整这类最极端情况的提案，它将大幅提高通过相对低廉的操作码和预编译公开的(传统)哈希函数的gas成本。为弥补这些gas成本的增加，我们可以降低证明起来较便宜的EVM操作码的gas成本，以保持整体吞吐量不变。
    • 替换数据结构 - 除了用更加STARK友好的替代物取代状态树之外，我们还需要替换交易列表、收据树和其他昂贵的证明结构。Etan Kissling提出的EIP，即将交易和收据结构迁移至SSZ([1] [2] [3])，就是朝这个方向迈出的一步。

除了上一节提到的两个"从帽子里变出的兔子"(即多维 Gas和延迟状态根)之外，它们也可以在这里提供帮助。但值得注意的是，与无状态验证不同，在无状态验证中，使用任何一个"从帽子里变出的兔子"意味着我们已经拥有了今天所需的足够技术，即使使用这些技术，实现完全的ZK-EVM验证仍需更多工作——它只是需要更少的工作。

另一个未提及的是证明者硬件:使用GPU、FPGA和ASIC来更快地生成证明。Fabric Cryptography、Cysic 和 Accseal是三家在这方面走在前列的公司。这对于第二层极其宝贵，但不太可能成为第一层的决定性考虑因素，因为有一个强烈的愿望使得第一层保持高度去中心化，这意味着证明生成必须在以太坊用户的一个相当大的子集的能力范围内，不应该受到某个公司硬件的瓶颈限制。第二层可以做出更加激进的权衡。

在每个领域都有更多的工作要做：

  • 并行化证明需要这样一种证明系统，在这种系统中不同部分的证明可以"共享内存"(如查找表)。我们知道执行这种操作的技术，但它们需要实现。
  • 我们需要更多分析来确定理想的一组gas成本变化，以最小化最坏情况下证明者的时间。
  • 我们需要在证明系统上做更多工作

这里可能的权衡包括：

  • 安全性与证明者时间:可能通过对哈希函数、使用更复杂或更激进安全假设的证明系统或其他设计选择的激进选择来缩短证明者时间。
  • 去中心化与证明者时间:社区需要就其所针对的"证明者硬件规范"达成一致。允许证明者成为大型实体吗?我们希望高端消费级笔记本电脑能够在4秒内证明一个以太坊区块吗?还是两者之间的某种状态?
  • 打破向后兼容性的程度:在其他领域的不足可以通过进行更加激进的gas成本变化来补偿，但这可能会使某些应用程序的成本大幅增加，迫使开发人员重新编写和重新部署代码以保持经济可行性。同样，这些"从帽子里变出的兔子"也有自身的复杂性和缺点。

它与路线图其他部分的关系 ​

实现在第一层进行EVM有效性证明所需的核心技术，与另外两个领域密切相关：

  • 第二层的有效性证明(即"ZK rollup")
  • 用于无状态化的"STARK a binary hash proof"方法

在第一层成功实现有效性证明后，可以实现最简单的单个质押：即使是最弱的计算机(包括手机或智能手表)也能够质押。这进一步增加了解决单个质押其他限制(如32 ETH最低值)的价值。

此外，在第一层的EVM有效性证明可以帮助实现大幅增加第一层gas限制。

共识有效性证明 ​

我们试图解决什么问题? ​

如果我们希望能够使用 SNARK 完全验证以太坊区块，那么 EVM 执行并不是我们唯一需要证明的部分。我们还需要证明 共识:处理存款、提款、签名、验证者余额更新和其他与以太坊 proof-of-stake 部分相关的系统部分。

共识比 EVM 简单得多，但它面临的挑战是，我们没有像第 2 层 EVM rollup 那样大部分工作都已经完成的理由。因此，任何实现证明以太坊共识的方案都需要"从头开始"，尽管作为支持的底层证明系统本身是可以重复使用的。

它是什么？工作原理是什么？ ​

信标链被定义为状态转换函数，就像 EVM 一样。状态转换函数主要由三部分组成：

  • ECADD 运算 (用于验证 BLS 签名)
  • 配对运算 (用于验证 BLS 签名)
  • SHA256 哈希运算 (用于读取和更新状态)

在每个区块中，我们需要为每个验证者证明 1-16 个 BLS12-381 ECADD 计算 (可能超过一次，因为签名可以包含在多个聚合中)。这可以通过子集预先计算技术来补偿，所以总的来说，我们可以说每个验证者需要一个 BLS12-381 ECADD 运算。如今，每个时隙都有约 30,000 个验证者进行签名。将来，在单时隙确定性的情况下，这个数字可能会有所变化(参见此处的说明)：如果我们采用"蛮力"路线，这可能会增加到每个时隙 100 万个验证者。同时，使用 Orbit ZK，该数字将保持在 32,768 个，或者甚至减少到 8,192 个。

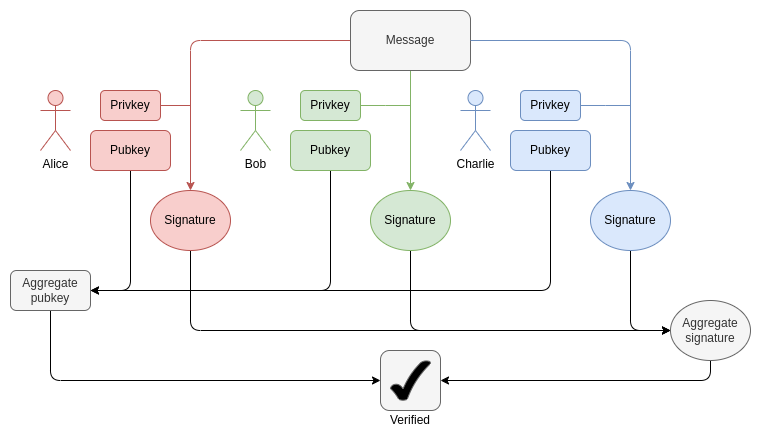
这解释了 BLS 聚合是如何工作的。验证聚合签名只需要每个参与者进行一次 ECADD 操作，而不是 ECMUL。但是，当参与者数量达到 30,000 时，即使是 ECADD 操作，其证明负荷也是相当大的。

对于配对(pairings)，目前每个时隙最多需要验证 128 次配对操作。随着 EIP-7549 及后续更改的推行，这一数字可望降至每个时隙 16 次配对操作。尽管配对操作的数量较少，但每次配对操作的运行或证明时间都是 ECADD 的数千倍，计算成本极高。

证明 BLS12-381 操作的一大挑战是，没有一条曲线的曲线阶数恰好等于 BLS12-381 域大小，这给任何证明系统带来了不小的额外开销。另一方面，以太坊提出的 Verkle 树是在 Bandersnatch 曲线 基础上构建的，这使得 BLS12-381 成为在 SNARK 证明系统中对 Verkle 分支进行证明的天然选择。一个相当简单的实现每秒可以证明约 100 次 G1 加法；但要让证明速度足够快，可能需要使用更高效的技术，例如 GKR(Groth-Koolen-Renes) 技术。

对于 SHA256 哈希，目前计算量最大的情况出现在 epoch 过渡块(epoch transition block)，这时整个验证者短余额树(validator short-balance tree)和大量验证者余额都需要被更新。验证者短余额树为每个验证者(假设总数为 100 万)存储一个字节，所以大约 1MB 的数据需要被重新计算哈希。这对应着 32,768 次 SHA256 调用。如果有一千个验证者的余额高于或低于某个阈值，需要更新在验证者记录中的有效余额(effective balance)，那就对应着一千个 Merkle 分支(Merkle branches)，再加上另外约一万次的哈希计算。打乱机制需要每个验证者 90 位(约 11MB 数据)，但这可以在一个 epoch 的任意时间内计算完成。随着单时隙确定性(single-slot finality)的引入，这些数字可能会再次增加或减少，具体取决于细节设计。虽然打乱机制变得不再必要，但 Orbit 方案可能会带来某种程度上的类似需求。

另一个挑战是需要读取所有验证者状态，包括公钥及其 Merkle 分支(用于证明公钥正确性)，以验证一个区块。单单读取 100 万个验证者的公钥就需要 48 百万字节的数据。这意味着每个 epoch(周期)需要计算数百万次哈希运算。如果我们今天就要实现股权证明验证，一个现实的方法将是某种形式的可增量验证计算：在证明系统内部存储一个针对高效查询优化过的单独数据结构，并证明对该结构的更新，以降低对于大规模验证所需的总体工作量。

总结一下，围绕信标链存在许多需要解决的挑战。

最高效地应对这些挑战可能需要对信标链进行深层次的重新设计，这个过程可能会与切换到单时隙确定性同时进行。这种重新设计可能包括以下特点：

  • 哈希函数变更:目前使用的是完整的SHA256哈希函数，由于需要填充，每次调用实际上对应着两次底层压缩函数调用。我们至少可以切换到SHA256压缩函数，从而获得2倍的性能提升。如果我们切换到Poseidon哈希函数，或许可以获得高达100倍的性能提升，这可能完全解决哈希运算所面临的一切问题：以每秒170万次哈希(54MB)的速度，即使有100万个验证器记录也可以在几秒钟内"读取"并生成相应的证明。

  • 如果采用Orbit，直接存储已混洗的验证器记录:如果选择一定数量的验证器(例如8,192或32,768个)作为某个时隙的委员会，可以将它们的记录直接连续存储在状态中，这样就最小化了将所有验证器公钥读入证明所需的哈希计算量。这种方式还可以高效地执行所有余额更新操作。

  • 签名聚合:任何高性能的签名聚合方案实际上都将涉及某种递归证明的过程，其中网络中的各个节点将生成子集签名的中间证明。这种方式自然地将证明的负载分散到了网络中的许多节点，从而大大减轻了"最终证明者"的工作负担。

  • 其他签名方案:对于Lamport+Merkle签名方案，我们需要进行256次哈希再加上32次哈希才能验证一个签名；乘以32,768个签名者，就需要9,437,184次哈希运算。通过优化签名方案，可以进一步提高一小部分性能。如果我们使用Poseidon哈希函数，即使在单个时隙内也有可能完成所有证明计算。不过从实际情况来看，结合递归聚合方案会让整个过程变得更加高效。

查看更多：现有研究资料链接

现有研究资料链接 ​

待解决的问题及权衡考虑 ​

从实际情况来看，在我们获得以太坊共识算法的完整有效性证明之前，还需要数年时间。这个时间范围大致与实现单时隙确定性、Orbit共识算法、更换签名算法，以及为了足够有信心使用"高度优化"的哈希函数(如Poseidon)所需进行的安全性分析，所需的时间相当。因此，目前最合理的做法是继续推进解决这些其他问题，同时在过程中时刻关注STARK友好性的需求。

主要的权衡取舍可能在于以太坊共识层改革的操作步骤，是采取渐进式方法还是一次进行多项大幅度改革。对于以太坊虚拟机(EVM)，渐进式改革无疑更为合理，因为这能最大程度减少对向后兼容性的影响。但对于共识层而言，向后兼容性的考虑较小，一次性进行全面重新设计各种细节的构建方式，以优化SNARK友好性，也许会更有益处。

它与路线图其他部分的关系 ​

STARK友好性需要成为以太坊权益证明共识长期重新设计的主要考虑因素，尤其是单时隙确定性、Orbit共识算法、改革签名方案，以及签名聚合等方面。

ETHStudy (An Ethereum Ecosystem Initiative)
Supported by Uweb(University of Web3)

Build Version 0.3.1